The Anthropomurphic Principle

MATHEMATICAL RECREATIONS by Ian Stewart

Scientific American, 1995

So wrote the poet James Payn in parody of Thomas Moore's lines about a gazelle in The Fire Worshippers. The event described is the archetypal instance of Murphy's Law: "if anything can go wrong then it will". Its origins lie in experiments carried out in the late 1940s by a USAF Captain (no prizes for guessing his surname). It has many variations and extensions, such as "even if it can't possibly go wrong, it still will," and it appears under other names than Murphy's.

In 1991 the British Broadcasting Corporation's TV series QED carried out experiments in which toast was tossed into the air under various conditions, and in every case obtained results statistically indistinguishable from pure chance. And there the matter might have rested, were it not for Robert Matthews. Matthews is a British journalist with a mathematical streak: a typical Matthews calculation starts with, say, a photograph of a building whose windows have blown out, and ends with an estimate of the wind speed. Writing in the European Journal of Physics (volume 18, 1995, pages 172–176) he observes that there are two problems with QED's experiments. Firstly, by its nature, Murphy's law may conspire to falsify any experiments aimed at testing it. Secondly, in the normal circumstances of eating breakfast, toast is not hurled randomly into the air. (OK, your family may have its own way of doing things, but the basic point stands.) Toast is generally knocked sideways off the edge of a table, and any experiments ought to mimic this fundamental circumstance.

Before proceeding, it is worth exposing one common misconception. The asymmetric behaviour of falling toast is not the result of the extra mass of butter. A typical piece of toast weighs about 40 grams, the butter is at most 10% of the total, and anyway it is mostly absorbed into the central regions. Its effect on the dynamics of the toast is negligible. And its effect on the aerodynamics of the toast, resulting from changes in surface viscosity, is even more negligible.

Matthews traces Murphy's law to a much simpler asymmetry: it is the top surface of toast that is buttered, and that surface remains on top when the toast is first nudged over the edge of the table. As the toast falls towards the ground, it rotates at an angular velocity determined by the degree of initial overhang of its centre of mass. Might it be the case that the height of a normal table and the Earth's gravitational force conspire to create a predominance of rotations through an odd multiple of 180 degrees? The short answer is that, according to Matthews's calculations, they do. In fact, a rotation that flips the toast over once, leading to a butter-down final state, is by far the commonest.

Box 1: The Murphodynamics of Toast. Define the overhang parameter \eta = (a + \delta) / a. Then Newton's laws of motion lead to the relation \omega^2 = \frac{6 g \, \eta \, \sin{\theta}}{a (1 + 3 \eta^2)} as long as the toast is pivoting about the edge of the table. The toast begins to slip when the frictional force at the table's edge is exceeded by the appropriate component of the toast's weight. Whatever the rotation rate is at that instant, the toast will therafter rotate at the same rate during its fall. The key variables are: \begin{array}{rcl} g &=& \mbox{acceleration from gravity} \\ m &=& \mbox{mass of the toast} \\ a &=& \mbox{half-width of the toast} \\ \delta &=& \mbox{initial overhang} \\ \theta &=& \mbox{angle of rotation} \\ \omega &=& \mbox{angular velocity of rotation} \\ H &=& \mbox{height of the table} \end{array} Simple estimates show that the toast will flip through at least 180º on the way to the floor. In order to land butter side up it must, therefore, rotate at least 360º. We know how fast the toast is rotating, and H (together with g) tells us how long it takes to hit the floor. For tables and toast of conventional dimensions, Matthews shows that it rotates at least 360º only when the critical overhang parameter \eta > 0.06. The critical overhang occurs when the toast first detaches itself and begins to fall freely.

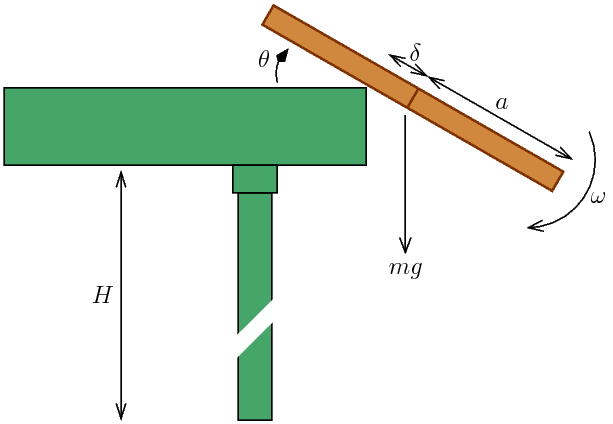
Before we consider the deeper reasons for this unhappy coincidence, it is worth summarizing the mathematical arguments that lead to this conclusion. The figure in Box 1 shows the initial configuration of the toast and the main variables involved, together with some key formulas derived from Newton's laws of motion. The main conclusion is that the toast cannot land butter-up unless the "critical overhang parameter" — the percentage of toast that hangs over the edge initially, relative to half the width of the toast — is at least 6%. Experiment shows that for bread the value is 2%, and for toast 1.5%. Both fall far short of what is required to make the bread or toast rotate through at least 360 degrees on its way to the floor. Since the rotation is provably at least 180 degrees, this implies that butter-down is the inevitable rule.

This analysis makes a number of assumptions. One is that the toast does not bounce when it hits. Since butter is highly viscous, this is reasonable: the normal outcome is a splat, not a boing. Another is that the toast slides slowly over the edge so that it detaches at the critical overhang value. A more detailed analysis shows that the horizontal velocity imparted to the toast as it goes off the edge of the table has no serious effect on the conclusions unless it is at least 1.6 m/sec, a fairly hefty wallop. This result does lead to a strategy for preventing butter-down descent: if you notice the toast sliding off the edge, bat it firmly with your hand to send it skimming across the room. This strategy is quite likely to have other adverse effects — for example, if the family cat is sitting at the point of impact — but it should avoid buttering the carpet.

This analysis is all very well, but it suggests that Murphy's law is merely a coincidence, a strange case of "murphic resonance" resulting from the rather arbitrary values that human culture assigns to tables and toast, in conjunction with the equally arbitrary value of the Earth's gravitational field. Matthews goes on to observe that nothing could be further from the truth. Murphy's law, as embodied in twirling toast, is a deep consequence of the fundamental constants of nature. Any universe that contains creatures remotely like us will necessarily inflict Murphy's law upon those creatures — at least if they eat toast and sit at tables.

The precise argument is technical and convoluted, but its outlines are simple. The key fact is due to W.H. Press, who argued in 1980 that the height of a bipedal organism is limited by the gravitational field in which it lives. Compared to quadrupeds, bipeds are intrinsically unstable: they are far more likely to topple because their centre of mass only has to stray outside their "footprint" for them to fall over. Quadrupeds have a much larger region of stability. (It is no coincidence that giraffes are taller than humans.)

The critical height is the one for which the impact of the head with the ground is likely to cause death. Of course this argument assumes that the crucial equipment is located at the top of the biped, but this does offer evolutionary advantages such as the ability to see further. (Half the fun in this kind of discussion is to make plausible assumptions and see where they lead. The other half, which I leave for readers to pursue, is to deny those assumptions and see where that leads.) It is also reasonable to assume that the height of table used by an intelligent biped will be about half the creature's own height. On Earth, a table needs to be about 3 metres high in order for Muphy's law to be violated, so we would have to be 6 metres high to escape the unfortunate consequences of murphic resonance. The deeper question is: might some race of aliens on some distant planet be murphically immune?

To answer this question, Matthews models said alien as a cylinder of polymer whose critical component is a sphere positioned at the top. I will call such an organism a polymurph. Death is occasioned by the shearing of chemical bonds in a polymer layer. His analysis leads to the conclusion that the height of a viable polymurph is at most

where n is the number of atoms in a plane across which any breakage takes place (typically about 100); q = 3 \times 10^{-3} is a constant related to polymers; f is the fraction of kinetic energy that goes into breaking the polymer bonds; \mu is the radius of polymeric atoms in units of the Bohr radius a_0; A is the atomic mass of polymer material; and \alpha is the electronic fine structure constant e^2 / (2 h \varepsilon_0 c), where e is the charge on the electron, h is Planck's constant, \varepsilon_0 is the permittivity of free space, and c is the speed of light. The constant \alpha_G is the gravitational fine structure constant 2 \pi G m_P^2 / (h c), where G is the gravitational constant and m_P is the mass of the proton.

Plugging in the relevant values for our universe we find that the maximum safe hight for a polymurph is 3 metres. (The tallest recorded human being [Ed. until 1995], by the way, is a certain Robert Wadlow, height 2.72 metres.) This is far short of the 6 metres needed to avoid buttering the kitchen carpet. Interestingly, this upper limit on polymuprh height does not depend upon which planet the alien inhabits. The reason is that the balance between internal gravitational forces and electrostatic and electron degeneracy effects, required for the polymurph not to fall apart, relates the planet's gravity to more fundamental constants. Thus we find that Murphy's law is not a coincidence at all, but the consequence of a deep "anthropomurphic principle:" any universe built along conventional lines that contains intelligent polymurphs will conform to Murphy's law. Matthews concludes: "According to Einstein, God is subtle, but He is not malicious. That may be so, but His influence on falling toast clearly leaves much to be desired."