Applied Math Enters the Digital Age

By Barry A. Cipra

SIAM News, December 17, 2007

Cry, baby, cry
Put your finger in your eye
--Mother Goose

Figure 1. The maximum force
a finger can apply in each of five
directions can be accurately
measured with a bead-embedded
thimble.

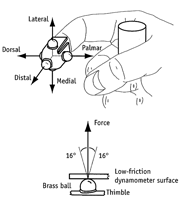
You've got to hand it to Francisco Valero-Cuevas. Not many grad students have the nerve to give their advisers the finger. In 1997, when Valero-Cuevas did so, it got him a PhD from Stanford. Now a professor of biomedical engineering at the University of Southern California, he described his extended applied mathematical studies of the human index finger in an invited address at the 2007 SIAM Conference on Applications of Dynamical Systems.

The human hand is a fascinating neuromuscular contrivance. Its ability to coordinate multiple degrees of freedom and act with simultaneous delicacy and force is the envy of roboticists. Structurally, each finger is a set of three hinged rods, connected by a complicated skein of taut, gristly strings to seven meaty actuators in the palm and forearm. (The only muscles in the fingers themselves are the ones responsible for raising goosebumps on the knuckles. Otherwise, finger flesh consists of a sack of skin housing fat and a mesh of capillaries, with a network of touch- and temperature-sensitive neurons on one side and a continuously extruding keratin plate on the other.) But the precise layout of tendons and their connections to the muscles is unlike anything a mechanical engineer is likely to concoct. Indeed, aspects of the tendon network have puzzled students of anatomy since the days of Leonardo da Vinci and the 16th-century anatomist Vesalius.

Valero-Cuevas and colleagues are beginning to get a grip on some of these anatomical mysteries. Combining laboratory experiments on human hands (some living, some cadaveric), mathematical analysis, and computer simulations, the researchers have shown that the intricate arrangement of muscle and tendon is key to human dexterity, the ability to grasp and manipulate objects by dynamically regulating force in any direction. Their research should help roboticists design more versatile mechanisms. It could also help surgeons restore more functionality as they repair injured hands; therapists could make use of it in developing and implementing rehabilitation regimens, and neurologists in understanding how disease, aging, stroke, and trauma impair hand function. Valero-Cuevas is looking for applied mathematics students to join his research efforts.

Manipulating a Hypercube
A cartoon model of a joint has a single muscle flexing the joint via a one-dimensional tendon. Because you can't (successfully) push a rope, another muscle–tendon pair is required for extension. If the two muscles are activated simultaneously, a process called "co-contraction," the result is the kind of pose body builders like to strike. Co-contraction sometimes helps stabilize a motion or posture. For some body parts, such as the elbow or knee, this cartoon model is fairly accurate. But not for the fingers.

We could have evolved a simple set of flexor–extensor muscle–tendon pairs for each knuckle. (Our fingers would have become longer and longer---albeit chunkier---with more and more joints.) But nature, for no obvious reason, took a different route. Opting to locate the muscles in the palm and forearm, at a distance from the fingers themselves, evolution tinkered its way to a quasi-two-dimensional system of interconnected tendons, more like fishing net than fishing line. This decidedly nonlinear and complex solution, anathema to "reasonable" engineering design, has paid off handsomely. With the force exerted by each muscle distributed throughout the network, the nervous system can do more with less: The fingers possess a tunable mechanics wherein coordination among the muscles produces the great repertoire of mechanical actions we call dexterity.

Roughly speaking, there are two steps in finger manipulation: getting the finger positioned properly and applying an appropriate fingertip force---taking hold of a grape, say, and then plucking it without crushing it. The transformation of muscle activation into static force at the fingertip boils down to a 4 x 7 matrix. The rows correspond to the three components of the force vector plus the (scalar) torque; the columns correspond to the seven muscles. If the model is normalized so that muscle activation ranges from 0 to 1, the "feasible wrench set" is a four-dimensional polytope obtained from the linear mapping of the seven-dimensional hypercube.

Actually, two of the seven muscles operating each finger are responsible primarily for ab- and adduction, the sideways movements that allow you to hold a cigarette and give the Star Trek Vulcan salute. The other five muscles operate the finger joints, a.k.a. knuckles. (Things aren't really quite this simply orthogonal, but it's a convenient first approximation.) Five muscles may not seem sufficient to flex and extend three joints---engineers typically use two motors per joint (one to flex and one to extend)---but in fact four would suffice: One muscle could act as a simultaneous extensor for all three knuckles, with variable amounts of co-contraction of three flexors taking care of the rest. Which raises the question: If nature could have gotten by with four muscles per finger, why splurge on five?

One short answer is versatility, or more precisely, the redundancy required by versatility. Versatility can be seen as the ability to apply at least a small amount of force in any direction; redundancy means that it can always be done in more than one way. The proof is straightforward: If each of the (small) wrench vectors w and –w corresponds to a non-negative combination of muscle activations, as versatility implies, then so does their sum, namely 0. A suitably small (but positive) multiple of this "active zero" can be added to any other point inside the activation hypercube, thereby giving redundancy at every point inside the feasible wrench set.

Another short answer is economy---more precisely, economy of effort. While four muscles suffice for any (planar) action of a three-hinge system, some of those actions might require inordinate exertion of one muscle. Physiologically, the body would be happier to have each muscle doing just a little work, regardless of the task at hand, or to have different muscles take over when others fatigue. By offering the central nervous system a continuum of options for carrying out any desired action, redundancy makes it possible to distribute the workload more evenly---the extra dimensionality of the muscle-activation hyper-cube is a cheap way to enlarge the feasible wrench set.

Redundancy also enhances the ability of fingers to compensate for injury. This is the exciting prospect for hand surgeons: A precise understanding of how muscular force translates into mechanical action will assist in the planning of procedures that leave patients with as much of their original range of motion as possible. (No doubt there will also be black-market demand for "dexterity augmentation" among card sharps and magicians.) Valero-Cuevas has collaborated along these lines with Vincent Rodney Hentz, a hand surgeon at the Stanford University School of Medicine.

Praemonitus Praemunitus
Just how versatile are the fingers? For his PhD dissertation, Valero-Cuevas measured maximum static force in five principal directions, using a simple experimental device: a thimble with metallic beads embedded on its surface, to be held against a low-friction force sensor (see Figure 1). The low friction ensured that the force would be applied directly at the sensor (actually within 16 degrees)---otherwise, the thimble would have slipped. The beads prevented torque---otherwise, the thimble would have rotated. In follow-up work with Charles Burgar (Valero-Cuevas's adviser), Felix Zajac, and Hentz, fine-wire electrodes were added to measure activation levels of the seven muscles (see Figure 2).

Figure 2. Each of the seven muscles controlling the index finger is activated to a different extent as the finger exerts force in different directions. Figures 1 and 2 reproduced with permission from "Large Index–Fingertip Forces Are Produced by Subject-Independent Patterns of Muscle Excitation," by Francisco J. Valero-Cuevas, Felix E. Zajac, and Charles G. Burgar, Journal of Biomechanics, 31 (1998), 693–703.

Researchers in robotics, accustomed to easy access to their systems' components, may find the latter study unremarkable. But working with live subjects is not so simple. A comment in Valero-Cuevas, Burgar, and Hentz's first report, of a study with 10 subjects and a total of 60 electrodes, is an indication of one excruciating difference: "Placement of the FWEs and contraction of muscles during force measurements were generally well tolerated. Only one electrode caused discomfort that became intolerable." Robots rarely complain when they're mistreated; AI has a way to go before its labs are targeted by its own creation, Processors for the Ethical Treatment of Automata.

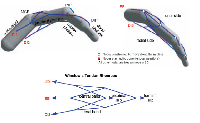
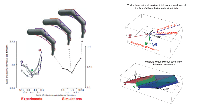
Some experiments are better done on the dead. Valero-Cuevas and colleagues have worked with donated cadaveric hands and forearms, opened to reveal the tendons, which they pull on with nylon strings connected to accurately measurable force actuators. Together with computer simulations, their experiments, in this case with the middle finger, show that the complex geometry of the tendon network permits greater dexterity than could be achieved with simple tendon paths. Experimentation of this type, which gave rise to anatomy and medicine more than half a millennium ago, is now being resurrected---with the help of sophisticated mechanics, mathematics, and control theory---to finish the work started by early anatomists.

An example is a rhombic structure first described by the 18th-century anatomist Jacob Winslow that is now known to embody the switching function of a logic gate. Winslow's rhombus distributes the tension from three muscles, labeled D12, D13, and EE in Figure 3, to the proximal and distal interphalangeal joints. Valero-Cuevas and colleagues have found that by varying the ratio of D12+D13 to EE while holding the total D12+D13+EE constant, they can get a V-shaped curve for the ratio of proximal to terminal "slip" tension, in both cadavers and computers (see Figure 4). Moreover, the feasible torque set changes in both size and shape with the distribution of tensions, suggesting that the hand's anatomy is responsible for the finer points of manipulation. (A one-muscle-per-bone system can alter the size of its feasible torque set, but not its shape.) In effect, the tendon network turns each finger into a computer that is literally digital.

Figure 3. Winslow's rhombus is a key component of the tendon network that distributes tension from the muscles to the phalanges.

Figure 4. Theory and experiments agree: The complicated tendon networks in fingers give rise to a form of digital computation.

The bottom line, Valero-Cuevas says, is that even static grasp is dynamic. As a demonstration during his talk, he had three volunteers stand around a glass bottle; each was to place a finger on the side of the bottle. When he asked them to lift the bottle off the table, they had no problem accommodating the request, each adjusting to the forces the others were applying. Then Valero-Cuevas asked them to walk across the stage. They didn't get far.