Fast Fourier Transform (FFT)
The fast Fourier transform (FFT) provides a way to compute the DFT, but
with computational complexity of 0(N log N)-
a very efficient algorithm. The modern approach is known as the Cooley-Tukey
algorithm, based on their paper from 1965 which described the algorithm (Tukey,
1965). However, it was later observed that the algorithm was known to Carl
Gauss (Heideman, 1985), probably around 1805. Between 1805 and 1965, there
were a number of rediscoveries of the approach. However, part of the reason
for the fame of the Cooley-Tukey result is that with the advent of computers,
computational approaches were much more tractable. So FFT would, from 1965
onward, become one of the most heavily employed algorithms of computational
science. We provide here only a short description of one key part of the
approach.
Let’s suppose that N is even. By definition, the DFT is given by
X_k = \sum^{N-1}_{n=0} x_n e^{-i2\pi(\frac{kn}{N})}, \qquad k=0,\dots,N-1.
(6)
We are going to separate the summation into two summations,
one which has the even numbered terms and the other with the odd numbered
terms. The easiest notation is to remember that if m = 0,1,...,
then 2m gives
all the even numbers and 2m + 1 gives
all the odd numbers. So we now rewrite Equation (6) by separating even and
odd numbered terms, so that
X_k = \sum^{N/2-1}_{m=0} x_{2m} e^{-i2\pi(\frac{k2m}{N})} + \sum^{N/2-1}_{m=0}
x_{2m+1} e^{-i2\pi(\frac{k(2m+1)}{N})}.
(7)
Because N is even, we can replace N/2 with
integer M. Additionally, by
factoring out e^{-(\frac{i2\pi k}{N})}
in
the second summation, we get
X_k = \sum^{M-1}_{m=0} x_{2m} e^{-i2\pi(\frac{km}{M})} + e^{-(\frac{i2\pi k}{N})} \sum^{M-1}_{m=0} x_{2m+1} e^{-i2\pi(\frac{km}{M})},
(8)
When K\geq M,
we note that each of the summations has a form that looks like of a DFT, with the first being a DFT on the even sample points, and the second being a DFT on the odd sampled points. We rewrite this result as
X_k = E_k + e^{-(\frac{i2\pi k}{N})} O_k,
(9)
Where Ek represents the DFT for even samples
and 0k is the DFT for the odd samples. These new DFT terms are now half the size, and all we have added is a single multiplication and a single addition. When K\geq M,
we observe that
e^{-i2\pi(\frac{km}{M})} = e^{-i2\pi(\frac{(k-M)m}{M})} e^{-i2\pi(\frac{Mm}{M})} = e^{-i2\pi(\frac{(k-M)m}{M})} e^{-i2\pi m} = e^{-i2\pi(\frac{(k-M)m}{M})},
where we take advantage of Euler’s formula from complex arithmetic:
e^{-i2\pi m} = \mbox{cos}(2\pi m) + i \mbox{ sin}(2\pi m) = 1 + i \cdot 0 = 1.
Then by suitable factoring, we find
X_k = E_{k-M} + e^{-(\frac{i2\pi(k-M)}{N})} O_{k-M},\quad k\geq M.
(10)
Note that in Equation (10), the term Ek - M is a term
that we have already computed for Equation (9) for some value of K\geq M,
similarly
for 0k - M.
To examine the issue of efficiency, we return to the idea of doubling the
number of sample points. When we double the number of samples, we simply
break the calculation into two problems of identical size as to what we had
before doubling. Our work, therefore, is doubled, but we must also include
the two operations (one more addition and multiplication) that are required
for each of the N terms. Let us consider a concrete example. Suppose we start
with N = 1024. We know
that this will require over 1 million additions and 1 million multiplications.
Instead, we make two problems of 512, which we turn into 4 problems of size
256, which we turn into … turns into 512 problems of size 2. The table
below outlines this computational complexity.
|
Basic Operations |
Compared to 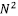 |
1 |
0 |
1 |
2 |
|
4 |
4 |
|
16 |
8 |
|
64 |
16 |
|
256 |
32 |
|
1024 |
64 |
|
4096 |
128 |
|
16384 |
256 |
|
65536 |
512 |
|
262144 |
1024 |
|
1048576 |
The table helps us to understand why it is “fast,” at least in comparison to DFT. Without the FFT, applying Fourier analysis to data is generally not practical.