Math Modeling
When facing a quantitative problem, whether it be in engineering, earth
and environmental sciences, medicine, or sports competition, a standard
first step is to find an appropriate mathematical model. This may require the
development of new equations, the construction of geometric models, the estimation
of several relevant physical quantities under different flow regimes, or the
analysis of uncertainty and parameter sensitivity.
A standard second step is to set up efficient and accurate numerical algorithms
for the approximation of solutions to the mathematical model. Once the problem
is solved by the computer (only rarely can a formula be found for solutions
to a complicated mathematical model), the numerical results need to be displayed
graphically and validated against experimental results. For sailboat design,
this step also includes understanding the level of turbulence around the various
yacht components, as well as the transition regions from smooth laminar flow
to turbulent flow as parameters, like the direction of sail relative to the
wind, are changed.
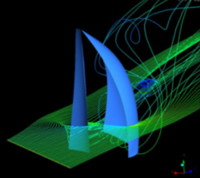 |
When dealing with downwind sails, streamlines visualization
can be extremely useful in order to detect whether (and where) the air
stream smoothly follows the sail surfaces or detaches to generate huge
vortices and turbulence. Even if wakes behind downwind sails can be usually
accepted (and often cannot be avoided), one of the main goals in order
to increase the driving force is to keep the flow stream attached to
the sail surface, and this can be obtained by means of a careful sail
design and a suitable trimming of the sail sheets as function of the
wind conditions (speed, direction, …).
Enlarge.
(Image courtesy of CMCS (Chair of Modelling and Scientific Computing-EPFL-Lausanne))
|
This second step led to mathematical problems consisting of more than 160
million equations and 160 million unknowns. Even though they were working with
a very fast computer at EPFL, mathematicians had to develop efficient algorithms
to solve such problems quickly. Moreover, the researchers had to solve these
equations many times. Parameters characterizing new shapes for the keel or
the position of the winglets on the bulb needed to be varied to see which would
produce the best results. In the end, the research group was able to run a
complete simulation of a new boat configuration in less than 24 hours.
Next comes a crucial third step. The modeling of complicated
real-world problems relies on feedback from testing to modeling to further testing
to provide a powerful and versatile tool. So once the Alinghi team
started training, the researchers were given suggestions on ways to improve
the whole design. Due to this interaction, simulations were needed until the
very final phase of the competition.
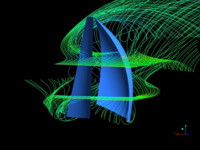 |
Detecting flow separation is also useful to check the
stability properties of sails. In fact, due to the strong non-linearity
of the Navier-Stokes equations, small variations of the inlet wind
speed and/or direction can significantly change the behavior of the
air stream, triggering abrupt flow detachments over some sail regions
and reducing separations over some others. Ideal sails should remain
reasonably stable under the effect of such perturbations, avoiding
large deformations and flutter. Enlarge.
(Image courtesy of CMCS (Chair of Modelling and Scientific Computing-EPFL-Lausanne))
|
Mathematicians also considered different scenarios for competition and studied
the interaction between the two opponent boats. Their analysis led to a decision-based
numerical tool that could suggest to the tactician ways to react in different
contexts.
The section "More Mathematics" provides more sophisticated details of the topics that were considered in the mathematics and the modeling.
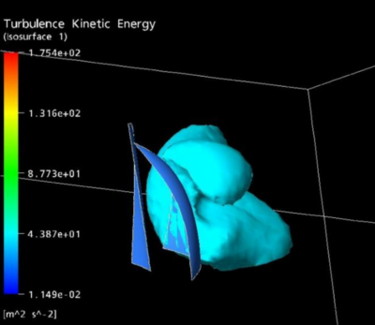 |
Visualization of turbulent kinetic energy can be an
important tool in order to check the size and intensity of the turbulent
structures around the sails. This 3D representation can be integrated
with other tools like the visualization of the velocity vectors and
the streamlines. This comparison helps to reach a deep knowledge about
the behavior of the involved physical phenomena and their complexity.
Enlarge.
(Image courtesy of CMCS (Chair of Modelling and Scientific Computing-EPFL-Lausanne))
|