More Mathematics

For performance optimization of an America’s Cup yacht, accurate numerical simulations of the flow around hull, sails, and appendages have been essential: the numerical solution of the mathematical equations governing the aerodynamics and hydrodynamics around the boat allows performance analysis in different sailing conditions (upwind and downwind), wind speeds, and yacht attitudes. Another important aspect is the interaction between fluids (air and water) and the structure (hull, appendages, sails, and mast). Moreover, the shape and dynamics of the so-called free surface (the interface between air and water) had to be accurately simulated in order to have a precise estimate of the wetted surface on the hull and henceforth of the yacht performance.

Advanced numerical simulations also played a crucial role in investigating sail aerodynamics. In downwind sailing, the flow around the sails presents wide regions of separated flow that cannot be adequately simulated using simplified numerical models, such as, for example, potential flow models. Three aspects of the problem have been considered: the force estimate on the sails, the aerodynamic interaction between boats sailing downwind, and the analysis of the shadow region generated by the windward yacht, which can adversely affect the progress of the leeward yacht. A complete mathematical model must take into account all these aspects characterizing the physical problem.

The mathematical problem is properly represented by the well known Navier-Stokes equations, which can describe the dynamics of any fluid of practical interest. Adding suitable interface conditions, the coupling between air and water is well posed and even if no general analytical solution is currently available, numerical solutions can be computed by exploiting the computational power of modern parallel computers. Enlarge. (Image courtesy of CMCS (Chair of Modelling and Scientific Computing-EPFL-Lausanne))

The Navier-Stokes equations for incompressible viscous flows were used to describe both water and wind dynamics. From one hand, they were coupled with elastodynamic equations for the simulation of the deformation of the big sails (the gennaker and the spinnaker) used in the downwind leg and, from another hand, with the free-surface equation that allows the determination of the water wave surface. Due to the very high Reynolds numbers that characterize these flow regimes, further equations need to be added for the determination of the turbulent kinetic energy, its rate of dissipation, and the transition between the region of laminar and turbulent flow.

In a very early phase of the design process, simplified models were adopted to reduce the overall computational complexity. These results were combined with experimental measurements obtained in the towing tank and wind tunnel to eliminate inefficient boat configurations. This step reduced costs and saved time.

During the second campaign all of the numerical algorithms for the flow simulation were refined. In addition, due to better domain decomposition algorithms and increases in computer speed, substantial improvements occurred in the study of the dynamical interaction between the sails and the wind.

When sailing upwind the fore sail is a flat and smaller Genoa and the fluid stream usually follows the sail surfaces. When sailing downwind the fore sails are the lighter, bigger and more deformable Gennaker and spinnaker and the fluid stream often shows large vortices and is highly turbulent. Thus, a fluid-structure interaction analysis on sails is much more complicated in the downwind case and must be modeled by a system of equations involving both the full Navier-Stokes equations for air and suitable membrane equations that properly describe the sail structures. Enlarge. ACM ag Stefano Gattini

Finally, statistical methods were employed to improve weather prediction during the race: high frequency variability was removed by smoothing and medium frequency was estimated by a random model. A stochastic approach was used to determine new lay lines (those delimiting the ideal route track towards the top mark): under stable wind these are straight lines issuing from the top mark, and the ideal strategy is a zig-zag sailing parallel to the laylines. Under shifty wind the ideal route should be redesigned according to a sort of stochastic laylines. This gave the navigator advantages that could be exploited during the regatta. The models told the navigator which side of the start line to use and when to tack during the upwind leg; they also described the wind behavior and proposed the fastest route.

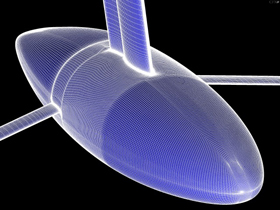
Bulb streamlines As with any lifting surface of finite span, the keel generates a tip vortex analogous to ones produced by airplane wings. This recirculation is associated to an additional component of the drag (the induced drag), which can be reduced by means of suitably designed winglets, whose placement over the bulb is itself a matter of careful design. Streamlines visualization helps to evaluate the effectiveness of such devices and to suggest new strategies to reach an optimal configuration. Enlarge. (Image courtesy of CMCS (Chair of Modelling and Scientific Computing-EPFL-Lausanne))

• America's Cup Home
• Legend of the America's Cup
• Math for Sailing
• Math Modeling
  • More Mathematics
• People Involved
• References and Links