How CAT Works: As Many X-rays as Possible
The secret to computerized axial tomography is to find out much more about the nature of the object than just its dimensions by looking at the attenuation of as many X-Rays as possible. To do this we need to think of a number of X-Rays at different angles \theta
and distances \rho from the centre of the object. A typical such X-Ray is illustrated below. 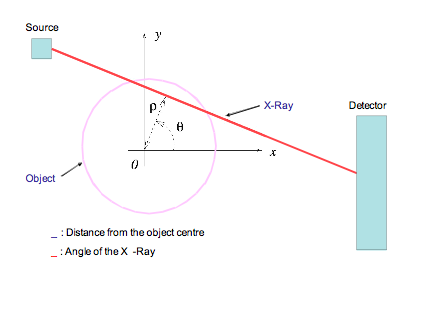
This X-Ray will pass through a series of points (x,y) at which the optical density is u(x,y). Using the equation for a straight line these points are given by
(x,y) = (\rho \mbox{ cos}(\theta) - s \mbox{ sin}(\theta), \rho \mbox{ sin}(\theta) + s \mbox{ cos}(\theta))
where s is the distance along the X-Ray. In this case we now have I_{\tiny\mbox{finish}} = I_{\tiny\mbox{start}} e^{-R(\rho, \theta)}
where
R(\rho,\theta) = \textstyle\int u(\rho \mbox{ cos}(\theta) - s \mbox{ sin}(\theta), \rho \mbox{ sin}(\theta) + s \mbox{ cos}(\theta))ds.
The function R(\rho,\theta) is called the Radon Transform of the function u(x,y).