Some Math
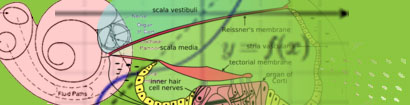
Our hearing organs developed over millions of years of evolution, moving in the general direction of species survival. Although they might no longer be tuned to help us avoid T-Rex, they are keenly refined to enable one of our primary specializations – the capability for a rich language of spoken communication. Crucial to understanding some rich sounds required for robust language is that different parts of the cochlea respond to different frequencies in the sound signal. The mechanical structure has been finely tuned so that it can precisely dissect the incoming signal, with distinct pitch patterns resulting in differing neural activity.
However, with a cochlear implant, we are bypassing that mechanical structure. Consequently, if we want the CI to allow the recipient to have rich language ability, we must process the sound signal into its frequency components to that locations along the cochlea can be correctly stimulated. That task is performed by the speech processor component of the CI. One of the functions of that processor is to act as a “mathematical cochlea” – the mechanical structure created by evolution will be replaced by mathematical algorithms. One of the most used approaches to separate a signal into frequency components is the Fourier
Transform. This mathematical approach and its numerical implementation will be our focus.