Tomography, GPS, and How to Land an Aircraft Safely
Right now a large number of GPS satellites are orbiting the Earth and transmitting radio signals down to the ground. If you can detect the signals and find the phase difference between the signals from several different satellites, it is possible to work out your location with a high degree of accuracy. GPS positioning methods are very widely used by aircraft navigation systems, SATNAV devices and hikers. However, one of the problems with this system is that variations in the ionosphere (the upper part of the Earth’s atmosphere) can affect the radio signals and change their phase by small amounts. This phase changer can lead to errors in the position given by the GPS system. These errors are not very large and are perfectly acceptable for navigating an airplane.
However, when landing an airplane it is vital that its height is known to a very precise degree and even small GPS errors can have large consequences. To do this we need to have an accurate understanding of the state of the ionosphere. There are many other reasons why understanding the ionosphere is important. Chief amonge them is the fact that the ionosphere has a very significant effect on the propagation of radio waves and on communication in general. Roughly speaking, lower frequency radio waves can bounce off the ionosphere, greatly increasing the range of a radio transmitter.
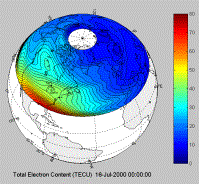
Remarkably, it is possible to monitor the state of the ionosphere by using tomography. In the problem of imaging a patient we transmitted X-rays through their body. To image the ionosphere, we use the transmissions from the GPS satellites recorded by special receivers. These form a very convenient set of "straight lines" passing through the ionosphere. The paths that they take are shown in the figure below.

The phase of the radio waves is affected by the electron content of the atmosphere, so that the total change in the relative phase between two frequencies is proportional to the change in the integral of the electron density along the ray path. If we can measure these phase changes, we can estimate the electron density integrals and work out the Radon Transform of the electron density. Thus we seem to be in exactly the same situation as the medical imaging problem and therefore we can work out the electron density at any point in the atmosphere. Well not quite.
There are two big differences between this problem and the CAT problem. First, the satellites are usually moving relative to the Earth. Secondly, there are large parts of the Earth’s surface where we cannot make any measurements. These include the oceans, where there are no receivers for the satellite signals, and the poles which do not have satellites orbiting above them. Thus we have a lot less information than we had in the case of the CAT scanner. This means that we are often in the situation of the milk deliverer who couldn’t distinguish between two different arrangements of milk bottles, each of which led to the same set of measurements.
In the case of the ionosphere, to get around this problem, we have to use a-priori information about the state of the ionosphere, or in other words a reasoned guess of what the solution should look like. This will allow us to reject one solution which doesn’t look like this guess and choose the solution which looks as much like the guess as possible. Fortunately, we understand the physics of the ionosphere well enough for our reasoned guess to be pretty close to the truth. By doing this (together with some other clever refinements), it is possible to use tomography to find the state of the ionosphere. In the figure below we illustrate a calculation (using the MIDAS software developed at the University of Bath) of an ionospheric storm (in red) developing over the southern part of the USA.