The Calculus of CAT
Imagine that the X-Ray moves along a straight line and that at a distance {s} into
the body it has an intensity {I(s)}. As {s} increases, {I(s)}
decreases as the X-Ray is absorbed. Now, if the X-Ray travels a small distance {\delta
s} its
intensity is reduced by a small amount {\delta I}
. This reduction depends both on
the intensity of the X-Ray and the optical density u(s)
of
the material. Provided that the distance traveled is small enough then the
reduction in intensity is related to the optical density by the formula
\delta I = -u(s)I(s)\delta s
Now, when the X-Ray enters the body it will have intensity I_{\tiny\mbox{start}}
and
when it leaves it has intensity I_{\tiny\mbox{finish}}
.
Using a bit of calculus we can combine all of the contributions to the
reduction in the intensity of the X-Ray given by all parts of the body
it travels through. Doing this finds that the attenuation (i.e. the reduction
in the intensity) is given by I_{\tiny\mbox{finish}} = I_{\tiny\mbox{start}} e^{-R}
where R = \textstyle\int u(s)ds
. This
is the attenuation of one X-Ray and it gives some information
about the body.
Below we see an object irradiated by several X-Rays with the intensity of the rays measured on a detector. Here, some X-Rays pass through the whole object and are strongly absorbed; their intensity, recorded at the center of the detector, is low. Others pass through less of the object and are therefore less strongly absorbed. Effectively, the object casts a shadow of the X–Rays and from this we can work out its basic dimensions. This is illustrated below.
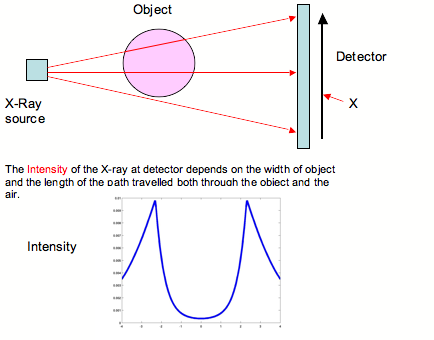The secret to computerized axial tomography is to find out much more about the nature of the object than just its dimensions by looking at the attenuation of as many X-Rays as possible.
