Radon Transforms
R(\rho,\theta) = \textstyle\int u(\rho \mbox{ cos}(\theta) - s \mbox{ sin}(\theta), \rho \mbox{ sin}(\theta) + s \mbox{ cos}(\theta))ds.
The function R(\rho,\theta)
is called the Radon Transform of the function u(x,y).
The larger R is, the more an X-Ray of this particular orientation
is absorbed. This transformation lies at the heart of CAT scanners and all
problems in tomography.
It was first studied by Prof. Johann Radon in 1917. (Radon is also famous for some very important discoveries related to the branch of mathematics called measure theory, which is the basis for integration.) By measuring the attenuation of the X-Rays from as many angles as possible it is possible to measure this function to a high accuracy.
The big question of mathematical tomography is then the problem of inverting
the Radon Transform i.e.
can we find the function u(x,y) if we know the function R (\theta,\rho)
.
(Incidentally, this is exactly the same problem faced by our milk deliverer). The short answer to this question is YES, provided we can make enough accurate measurements. A complete explanation of this (together with a quick way of calculating R(\rho,\theta) will
be given in the next section. However, a quick motivation can be shown by
the following example. In the two figures below we see on the left, a square,
and on the right, its Radon Transform in which the large values of R(\rho,\theta)are
shown as darker points.
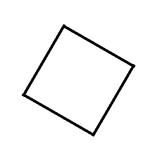
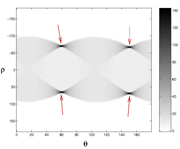
The key point to note in these two images is that the four straight lines making up the sides of the square show up as points of high intensity (arrowed) in the Radon Transform. The arrowed points give both the orientation of the lines and their distances from the center of the square. The reasons that lines give large values for R at certain points is that an X-Ray passing straight through a line is strongly absorbed, whereas one that misses it, even slightly, is hardly absorbed at all. Basically, the Radon Transform is good at finding straight lines in an image.
One method for finding u(x,y), called the filtered back projection algorithm, works (roughly) by assuming that the original image is made up of straight lines and to draw those corresponding to the high values of R. This method is fast but not particularly accurate. However, it is possible to find u(x,y) accurately and quickly, and algorithms to do this are implemented in the scanning devices. The original development of such devices used a mathematical object known as Fourier transform to invert Radon transforms. If you're up for some serious maths, read the section on how this is done. Most of the maths here is university level, but the section contains some lovely mathematical ideas.