Solving the Milk Delivery problem
Problem:
Milk and fruit juice is delivered in bottles which are placed in trays with nine compartments arranged as a 3x3 grid. Each compartment of the tray contains a bottle which may be empty, or may contain milk or juice. The question is: which type of bottle is in which compartment? Unfortunately we find ourselves in a situation where we can’t look down on top of the tray because other trays are on top of it and underneath it.
At first sight it would seem impossible to solve this problem. However, we can peer in through the sides and measure how much light is absorbed in different directions. Different types of bottles absorb different amounts of light. Careful measurements have shown that milk bottles absorb three units, juice bottles two unit, and empty bottles one unit. If a light beam is shone through several bottles, this absorption adds up. For example, if a light beam shines through a milk bottle and then a juice bottle five units are absorbed, and if it passes through three empty bottles, three units are absorbed.
Here is an example in which we have indicated the total amount of light absorbed by shining light through each of the rows and each of the columns (so that five units are absorbed in the first row and six units in the first column).
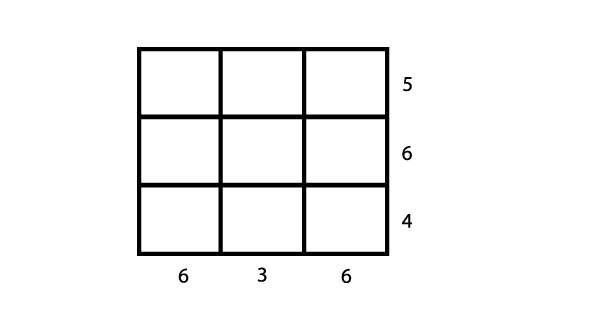
Can you work out from this information which bottles are in which compartments? To solve this puzzle you must place a bottle with one, two or three units of light absorption in each compartment with the sum of the units in the first row equaling five, the second row six, and so on. To start solving this puzzle we can see that the middle column contains three bottles and also absorbs three units of light. The only way this can be done is for each compartment of the middle column to contain one empty bottle, each absorbing one unit of light. What about the other compartments? Unfortunately we don’t have enough information to solve this puzzle; there are two different solutions:
3 1 1 2 1 2
2 1 3 2 1 3
1 1 2 2 1 1
We are faced with a rather unusual situation for a mathematician: that there are two perfectly plausible solutions to the same problem. Problems like this are called ill posed and are common in situations where we are trying to extract information from an image. To find out exactly how the bottles are distributed we need to have a little more information. One obvious extra thing that can be measured is the light absorbed in the two diagonals of the tray. By doing this, we find that six units are absorbed in the top-left/ bottom-right diagonal, and three units in the bottom-left/top-right diagonal. From this, it is clear that the first solution, and not the second, corresponds to the measurements made. It can be shown with further math, that if we can measure the light absorbed in the rows, columns, and diagonals exactly, then we can uniquely determine the arrangement of the bottles in the compartments of the tray.
This problem may seem trivial, but it is very similar to the medical imaging problem that will be described in the next section. It also shows how important it is to obtain enough information about a situation to make sure that we know exactly what is going on.