Milk Deliveries and Killer Sudoku
Before delving into the depths of medical science, we will start with a simple example which illustrates the principles of tomography, and which has a very nice link to the various types of Sudoko that have recently become popular.
This example involves milk deliveries. Imagine that milk and fruit juice is delivered in bottles which are placed in trays with nine compartments arranged as a 3x3 grid. Each compartment of the tray contains a bottle which may be empty, or may contain milk or juice. The question is: which type of bottle is in which compartment? Unfortunately we find ourselves in a situation where we can’t look down on top of the tray because other trays are on top of it and underneath it.
At first sight it would seem impossible to solve this problem. However, we can peer through the sides and measure how much light is absorbed in different directions. Different types of bottles absorb different amounts of light. Careful measurements have shown that milk bottles absorb three units, juice bottles two units, and empty bottles one unit. If a light beam is shone through several bottles, this absorption adds up. For example, if a light beam shines through a milk bottle and then a juice bottle, five units are absorbed. If it passes through three empty bottles, three units are absorbed.
Here is an example in which we have indicated the total amount of light absorbed by shining light through each of the rows and each of the columns (so that five units are absorbed in the first row and six units in the first column).
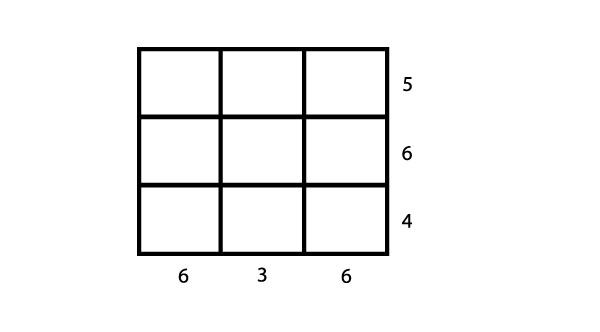
From this information, can you work out which bottles are in which compartments? To solve this puzzle, you must place a bottle with one, two, or three units of light absorption in each compartment with the sum of the units in the first row equalling five, in the second row six, and so on.
This problem may seem trivial, but it is very similar to the medical imaging problem we will describe in the next section. It also shows how important it is to obtain enough information about a situation to make sure that we know exactly what is going on.